EDMA 262 Mathematical journal

EDMA262

Georgia Butler’s Weekly Mathematical Reflections:

Week One Reflections

The Big Idea:

Understanding of what mathematics and numeracy are.

A pedagogical model for the teaching and learning of mathematics.

The difference between concepts, skills and strategies.

What is ACARA mathematics?

Mathematics is a language. Within this language model there are concepts, skills and strategies (Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S., 2012) for a student to fully grasp mathematics, they need to understand each topics strategies, concepts and skills. The teacher needs to decide what the appropriate level of understanding to model is. This is done through teaching the student the mathematical concept, skill or strategy. A concept within mathematics is the ‘why’ or the ‘big idea’. It is the workings behind the students answer. A mathematical skill is number sense, representation, spatial sense, measurement, estimation, patterns and problem solving. These are all examples of mathematical skills. A mathematical strategy is the way the content is taught. An example of this would be making it hands on, using visuals, differentiating learning, asking the students to explain their ideas and incorporating real world connections into the math stories.

Personal Reflection:

As a future teacher I want mathematics within my classroom to be deemed as enjoyable as every other subject. I do not want my students to groan when they are asked to pull out their maths books. I believe that in order for children to understand mathematics and have a positive mind set towards it, they need a role model that advocates it. As a future teacher, I will strive to put a positive spin on mathematics. This would be done through interesting lessons, choosing the right pedagogical approach and learning what stage the children are in the mathematical language model.

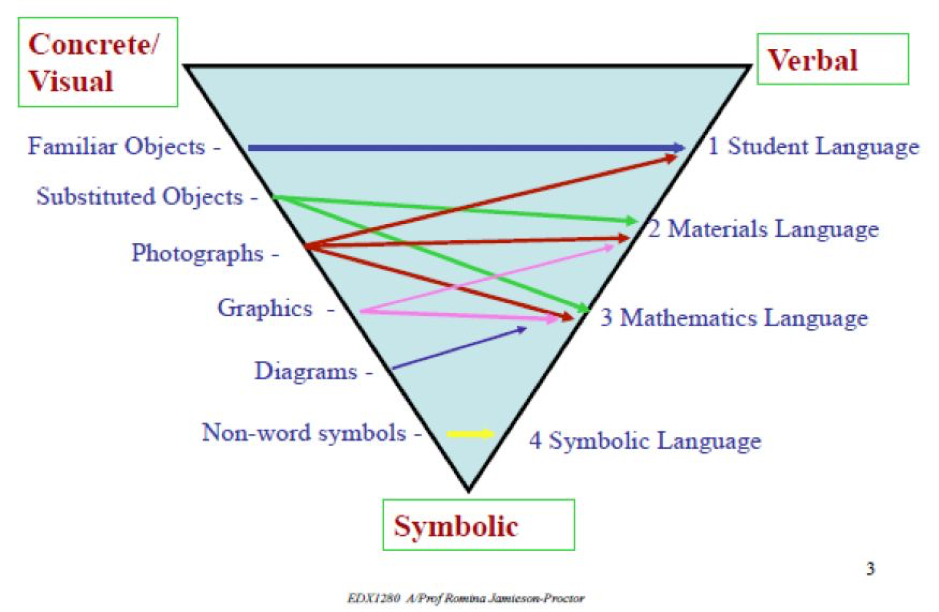
Mathematical Language Model:

Children have four levels of learning within this model. The levels are known as student language, materials language, mathematics language and symbolic language. The first level: student language stage; this is where a student is taught using familiar words and objects. The second level: Materials language, this is where substituted objects, photographs and graphics are used. The third stage is: Mathematic language; this is where graphics, diagrams and no symbols are used. The final stage is the symbolic stage; this is where there are no word symbols that are used.

ACARA Definition:

The Australian Curriculum: Mathematics aims to ensure that students are:

• Confident
• Creative users and communicators of mathematics
• Able to investigate, represent and interpret situations in their personal and work lives and as active citizens.

Learning mathematics creates opportunities for and enriches the lives of all Australians. The Australian Curriculum: Mathematics provides students with essential mathematical skills and knowledge in number and algebra, measurement and geometry, and statistics and probability.

Week Two Reflections

The Big Idea:

Addition

When teaching mathematics, the teacher needs to be aware of the importance of language development. The key to teaching a student successfully within mathematics is through language. By looking at the language model for mathematics, it shows the four language stages a student must acquire. These stages all need to be met in order for the student to fully understand mathematics. (Reys, et al. 2012) Through the use of all three concepts, skills and strategies combining, the student will be able to confidently demonstrate their own understanding of mathematics. For this week, the focus topic is addition.

Reflection on Mathematical Language:

I had never considered that mathematics was a language of its own. I am now coming to terms with the understanding that students need to be aware of the language of mathematics, before they can even consider understanding the symbolic language of mathematics. As a pre-service teacher, I believe that all stages within the mathematical language are important. Within all of the stages the student is making meaning within their minds.

Concept of Addition:

To ensure that all the students understand the addition concepts, I would introduce it to them through the games and real-life examples. Addition is commonly known as the concept of joining things together. This small concept is the beginning of many students understanding of mathematics. That is why it is crucial to have evidence of this concept within the classroom. Whether it be found through additional story books, mats, card games, songs or puzzles. These resources promote the concept of addition within the classroom for students by using real world examples.  

Examples of Addition Concepts:

• Addition mats
• Engage in discussion (Children language stage) when teaching the concept of addition
• Be descriptive when using the addition mats. Addition mats visually display to the process of addition to the students.

Language Model for Mathematics in Relation to Addition:

	Children’s Language Stage	Material’s Language Stage	Mathematics Language Stage	Symbolic Language Stage
Language	‘Put with’ and ‘How many bears do I have altogether?’	‘Add’ and ‘equal’	‘Add’ and ‘equal’ ‘I have two bears and I add three bears. How much does this equal?’ ‘Plus’ ‘how many more?’ ‘all up’ ‘in total’ ‘bigger than’	At this stage the students would be introduced to the symbol for addition and the equals sign. This would be the + symbol for adding and the = symbol for equals.
Materials	For this stage the children would be shown counting bears.	For this stage the students would be shown counters or books.	For this stage the students would be asked a number story.	For this stage the students would just be shown the symbols for the equation.
Recording	No symbols, drawing pictures only	No symbols, drawing pictures only	No symbols, drawing pictures only	1+1=2

Student Misconceptions:

Within the classroom, a misconception occurs within mathematics when a student has not fully understood a mathematical operation. In relation to the concept of addition, a student may misunderstand that

ACARA Links: Lower Primary Years:

Foundation Year:

• Represent practical situations to model addition and sharing (ACMNA004)

Year One:

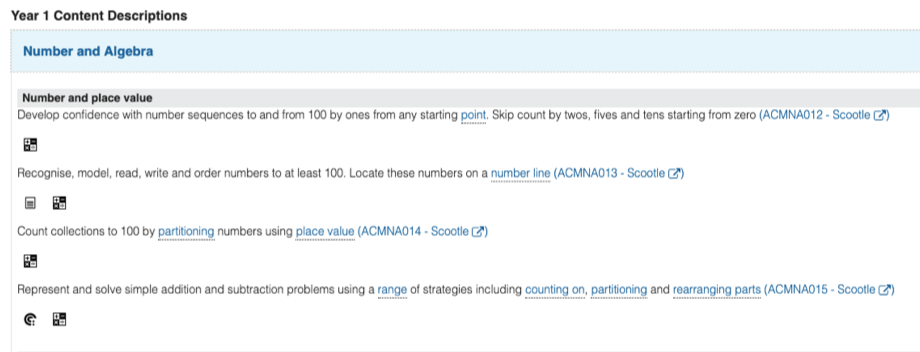
• Represent and solve simple addition and subtraction problems using a range of strategies including counting on, partitioning and rearranging parts (ACMNA015)

Year Two:

• Solve simple addition and subtraction problems using a range of efficient mental and written strategies (ACMN030)

Scootle Resource:

This Scootle activity would be best suited for students that are in their foundation year. The key learning objective for this activity is for the students to solve the addition problems by using a range of counting strategies. This resource would be for students in the student language stage of the mathematical language stage. This activity also uses the symbolic language stage. However, if the students had not reached the symbolic stage the teacher could help, or they count skip this step within the activity. (ACARA, 2019) (Scootle, 2019)

http://www.scootle.edu.au/ec/viewing/L8281/index.html

Figure 1: Counting Beetles: Level One Mathematics

Sourced Resources:

The game ‘Race to The Moon’ could be a great game to play within the classroom for the students. This resource is at the symbolic language stage of the mathematics language model. The game consists of additional sums that are symbols. It would be a fun way for the students to learn how to quickly add numbers together. For this resource the students would need to be able to know the symbols of add (+) and equals (=). The aim of the activity is for the students to go as quickly as they can through the additional equations, until they reach the top. My only caution for using this resource is that it would require the student to be in the symbolic stage of the language model for them to attempt it.

https://www.math-salamanders.com/math-addition-games.html

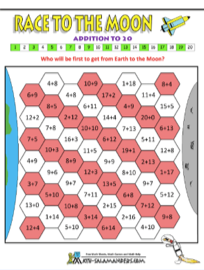
Figure 2: Race to the Moon

Textbook Reading:

Within the textbook (Reys et al., 2012) it refers to additional strategies within chapter nine. This gives an example of how to teach the content of addition. A good example of the strategy of teaching addition was evident in the ‘adding to 10 and beyond strategy’. This was outlined and I believe it is a perfect example of how lower primary years can learn how to add on numbers. As a future teacher, this strategy is a way in which I can teach addition to my students.

Week Three Reflections

The Big Idea:

Subtraction

When a student is learning subtraction, they need to be taught that it isn’t just taking away. There are three types of subtractions within mathematics. The first is ‘take away’, ‘difference or comparison’ and lastly ‘missing addend’ (Reys, et al. 2012). Along with this week’s topic of subtraction, the other big idea was the difference between mathematics and numeracy. Mathematics is what the educators teach the students (mathematical symbols, language and numbers), whereas numeracy is the student’s ability to use mathematics in their daily life (ACARA, 2019).

Outcomes-Based Education and Students Learning Outcomes (SLO):

As a future teacher, I’m well aware that all students learn differently. That is why it is important that the three types of subtraction are taught to the students. This ensures that there is a greater chance of the students understanding at least one of the concepts. Having different options and learning paths for subtraction enables the students to be in control of their learning. They can decide which concept they wish to use to solve the question.

Subtraction Concepts:

Subtraction can be defined as the operation that lets us know the difference between two numbers (Burnett, J., Irons, C., & Turton, A., 2015). This mathematical concept informs the student how many are left after something is taken away (Reys, et al. 2012).

Take Away: ‘I had $4. I then bought a toy for $3. How much money do I have now?’

Difference and Comparison: ‘My friend has three chocolates and I have one chocolate. How many more chocolates does my friend have?’

Missing Added: ’The toy I want is $7 and I have $5 in my purse. How much more money do I need to have the right amount for the toy?’

(Cockburn, A. D., 2007)

Personal Reflection:

It is highly important an educator is aware of the difference between mathematics and numeracy. The teacher needs to know the order in which they are to introduce this concept to their students. They need to be aware of the mathematical language stage in which their students are in. The focus should be to introduce this new concept to the students in a way that is simple, easy to understand and focuses on the students learning outcomes. I feel as though my knowledge on the concepts of subtraction and the difference between numeracy and mathematics I can see why the language acquisition model is so important. By being aware of the many different ways one can use and teach subtraction, I believe that this gives me a greater understanding on teaching the topic. This has been done by engaging in the content and fully understanding the different forms of subtraction.

Language Model for Mathematics in Relation to Subtraction:

Language Stages	Materials	Language	Recording
Student’s Language	Counting bears may be used.	‘How many do I have/ have left?’	No symbols, children drawing pictures only.
Materials Language	Counting bears can still be used, along with drawings and books.	‘Give’ and ‘How many do I have?’	No symbols, children drawing pictures only.
Maths Language	Subtraction books would be used.	‘Subtract’ ‘equals’ Minus’ ‘take away’ ‘smaller than’ ‘less than’	No symbols, children drawing pictures only (including maths materials). May write word stories.
Symbolic Language	None should be needed.	Symbols would be used.	5-3=2

Student Misconceptions:

A common misconception that many students face when learning subtraction is ‘only understanding subtraction as taking away’. Subtraction is first introduced to a student as taking a something away. However, this enables the student to create a tangible connection. This works when the numbers are small and positive. Although, when a student is introduced to larger or negative numbers they begin to run into some problems. If they are given a problem such as 0-10, they might ask ‘How can you take away from 0’. They cannot physically ‘take away’ another object. They will need to understand that they just keep counting back into the negative integers to arrive at a solution. However, this confusion can be avoided. This can be done through teaching the student that subtraction is more than just ‘taking away’. They need to understand that subtraction is also that when you subtract two numbers, you find the difference between the two. (APASS education, 2019)

ACARA Links: Lower Primary:

Foundation Year:

• Represent practical situations to model addition and sharing (ACMNA004)

Year One:

• Represent and solve simple addition and subtraction problems using a range of strategies including counting on, partitioning and rearranging parts (ACMNA015)

Year Two:

• Solve simple addition and subtraction problems using a range of efficient mental and written strategies (ACMN030)

Scootle Resource:

The Scootle resource is called number trains. This resource would be used after the students had developed an understanding of the concepts of subtraction. This resource has levels of hardness and incorporates numbers and counting. This type of activity would best be suited for lower primary years, whom are in the mathematical language stage of the mathematical language model. This activity uses numbers and general number words that the students would be familiar with if they are in this language stage. (ACARA, 2019) (Scootle, 2019)

http://www.scootle.edu.au/ec/viewing/L2317/index.html

Figure 3: Number Trains

Sourced Resource:

This resource is called ‘subtraction mayhem to 12’. This game would best be suited for student that are in the symbolic stage of the mathematical language model. This game would be ideal for grade two. It uses symbols such as minus (-) and equals (=). The students would need to have knowledge on the concept of subtraction. A caution for this activity is that the student would have to be at the symbolic stage of the language model. This would be an activity given to the students once they understood symbols and how to complete the equations.

https://www.2nd-grade-math-salamanders.com/subtraction-games.html

                                                                 Figure 4: Subtraction Mayhem

Textbook Reading:

A strategy that was present within the textbook (Reys et al., 2012) was partitioning. This strategy included the student breaking the number up and knowing what makes up the number. An example of this would be:

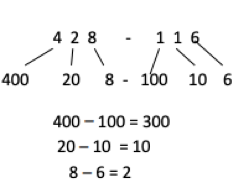
As seen in the example, the student would break up larger numbers to make it easier. If the student is familiar with the whole number, it might make it easier for them to work out the equation. This strategy would be useful for students in the symbolic stage of the mathematical language model.

Week Four Reflections

The Big Idea:

Multiplication: Mathematical Properties, Lowest Common Multiples and Greatest Common Factors

Multiplication is when you add a number to itself a specified number of times. The multiplication of 7×5 is to add seven to itself five times (Wells, D., 2012). For a student to understand the concept of multiplying an integer, they need to understand fully the concept of addition. That is why a student needs to learn specific mathematical concepts first, in order to learn complex mathematical concepts.

Personal Reflection:

As a future teacher, I want my students to find multiplication simple to learn. I want to correlation between addition and multiplication to be apparent to my future students.

The Concept of Multiplication:

The concept of multiplication consists of four ways: The set model, the array model, the measurement/ length model and the combinations model. When the teacher first introduces the concept of multiplication to the students, it would be in the form of the student’s language stage. Within this stage the students would use the words such as ‘groups of’ and ‘cups of’. By using real life terms, the students would find it easier to grasp the concept of multiplication. As seen in the language model for multiplication, the students would be shown objects they are familiar with until they reach the symbolic language stage. In this final stage, the students would just be given symbols for the mathematical equation.

Language Model for Multiplication:

Language Stages	Materials	Language	Recording
Student’s Language	Groups of people, lollies, fruit (grapes)	‘How many are there all together?’	No symbols, children drawing pictures only.
Materials Language	Lollies, counting bears	‘How many do I have all together?’	No symbols, children drawing pictures only.
Maths Language	MAB blocks, cubes	‘Multiplied by’, ‘by’, ‘equals’, ‘together’, ‘total’	No symbols, children drawing pictures only. Children may write mathematical word stories.
Symbolic Language	No materials would be used at this stage.	5×4=20	3×5=15

Student Misconceptions:

A common misconception that students have with multiplication is that they assume the result will always be a larger value. This common misconception is because students are taught that multiplication is like addition. They are taught to repeat addition. Students are able to generalize that the product of two values will always be greater than both the multiples. However, this assumption is only valid when it is two whole numbers. When a decimal or fraction is introduced, the student won’t understand why multiplying a fraction and a whole number creates a smaller value. This is also the case for negative numbers being multiplied together. Students need to be taught when they can and cannot just repeat addition. Repeating addition is good at the start of learning multiplication; however, the students need to be taught that this isn’t always the approach to use with multiplication. (APASS education, 2019)

ACARA Links:

Scootle Resource:

The Scootle resource is called ‘Sites2See’ and is a resource for foundation, year one, year two, year three, year four, year five and year six students. This activity covers multiplication, division, subtraction and addition. This activity would be used for students that are in the symbolic stage within the mathematical language model. This activity would require the students to understand the topics of addition, multiplication, subtraction and the teacher would choose to leave division out if the students had not yet covered this topic.

https://app.education.nsw.gov.au/rap/resource/access/31a8127a-1b93-4538-b463-2a71bb1a0e41/1

Figure 4: Subtraction Mayhem

Sourced resource:

This activity would best be suited to students with grade three, four and five. This activity would require the students to be in the symbolic language stage of the mathematical language model. That is due to it having numbers and the students would need to be able to multiply by using numbers and symbols. A caution for this activity would be that the students need to understand multiplication fully before they could engage in this activity.

https://www.teacherspayteachers.com/Product/FREE-Penguin-Multiplication-Dice-Game-1577809

Textbook Reading:

A strategy in relation to multiplication within the text book (Reys et al., 2012) is ‘commutative’. This is the idea that two numbers can be multiplied in either order. Once a student is taught this strategy, it simplifies a range of equations within multiplication.

Week Five Reflections

The Big Idea:

Division: Position and Quotation, Thinking Strategies and the Close Relation to Multiplication and Prerequisites Necessary to Understand Division.

Division is commonly known as how many times one number (the divisor) is able to go within another number (the divided) (Division in Mathematics, 2001). This week’s topic all relates to division. The students need to fully understand the concept of division and its mathematical language which is spoken. Students need to understand that when dividing they’re inversely multiplying. After learning multiplication, students can then fully understand division. They need to understand the thinking strategies used and positions and quotations.

Personal Reflection:

As a future teacher, I will make sure that my students understand the relationship between learning multiplication and learning division. It will make it easier if the students are aware of this relationship. When a student learns to multiply, they add quantities of numbers together. However, when a student learns how to divide, they need to be able to know how many groups go into one number. Students will find division simple if they fully understand multiplication. The students also will need to be aware that division has multiple ways of being shown in symbols. As a future teacher, I would need to be aware of all these symbols and present them to the students.

The Concept of Division:

The concept of division involves separating a number into two equal parts. This is known as parting (sharing) and quotation (repeated subtraction). Division can be shown in two ways:

Partition: When you have a larger number and you divide it into groups to see how much are in each group. Example: You have ten chocolates and there are five people. How many chocolates can each of you have?

Quotation: This is when repeated subtraction occurs to find the number of groups needed to divide up the total. Example: You have ten chocolates and you give two chocolates to each of your friends, so how many friends do you have?

Language Model for Division:

Language Stage	Materials	Language	Recording
Children’s Language	Stories, toys, division games, stories, nursery games and pictures.	Fair, sharing, subtraction, equal, same as, take away	No symbols, drawing pictures only
Materials Language	Books, counters, MAB blocks, cubes, buttons, marbles	Sharing, fair, equal parts, take away	No symbols, drawing pictures only
Maths Language	Books, counters, MAB blocks, cubes, buttons, marbles	Divide, division, how much, equals, divide into	No symbols, drawing pictures only.
Symbolic Language	None should be needed	24 divide 3. Halving. Introducing symbols.	6/6=12

Student Misconceptions:

Misconceptions occur within division when students are learning within the student language stage of the mathematical language model. Students build this misconception that when they divide, they think they repeatedly add equal numbers, instead of realising that they need to separate the total into equal parts. Teacher can sometimes represent division to students as ‘filling in’ the total. This is demonstrated in the question ‘How many 3’s go/ fit into 6?’ A way to change this would be to instead ask the students ‘How many 3’s can I get out of 6?’ It is crucial that a teacher does not let their students form misconceptions when they are learning division. If misconceptions are formed, it becomes difficult for students to fully understand the concept.

ACARA Links:

• 

Scootle Resource:

This resource would be ideal for students in grades five and six. It would be aimed at students whom are in the symbolic language stage of the mathematical language model. This resource enables students to solve division problems from dividends between 2 and 99. This activity enables the students to link between division and multiplication.

http://www.scootle.edu.au/ec/viewing/L3704/index.html

Sourced Resource:

This activity would best be suited for grade threes that are in the symbolic stage of the mathematical language model. This activity would involve the students solving the problems in order to colour in the picture. The caution for this activity would be for if a student didn’t know the names of the shapes. They might find it difficult to fully engage in the activity.

Textbook Reading:

A useful strategy within the textbook was for the student to ‘think multiplication’ when they came across a division question. An example of this would be 10/20. The student would be asked ‘what times 10 equals 20?’ They would have to either trial and error or add up the numbers to work out their answer. This would be a good strategy to teach students when they had a good understanding of multiplication. 

Week Six Reflections

The Big Idea:

Pre Number and Early Number Concepts

Sorting By Six Different Attributes

The Main Five Counting Principles

Pre-numbers are used for students to understand mathematics before they engage in numbers. The pre-number stage uses words such as sorting, matching, ordering and comparing. The pre-number stage uses words such as sorting, matching, ordering and comparing. Pre-numbers provide prerequisite knowledge to commence the study of numbers. Student’s need to understand patterns in order to grasp an early number understanding. Students also need to be able to know all five counting principles and know subtilizing.

Personal Reflection:

I personally had not realized that pre-numbers were a thing. I had also never known of the five counting principles. As a future teacher, I am now aware of the importance of pre-numbers and the five counting principles.

Concept of Pre Numbers:

The concept of pre-numbers is to sort numbers into groups. This is done by having a larger number and grouping it into smaller parts. Pre-numbers is when a student can define the attributes and sort certain objects. An example of this is when a student divides a packet of lollies, the student would look at the colours, sizing and shapes of the lollies and sort them into groups accordingly.

When introducing students to the concepts of pre-number, there are six concepts:

Determining Attributes – children firstly need to learn what an attribute or a characteristic is before they can move on to the process of matching, sorting, comparing, ordering and making patterns. Educators need to encourage them to use all of their senses when determining the attributes, and to get into the practice of recognising, and naming them.

Matching By Attributes -the concept of matching is comparing 2 objects looking for sameness. They could be identical (a perfect match) but they may not.

Sorting By Attributes – the concept of sorting is grouping a large number of objects into smaller groups and being able to describe the attributes upon which they were sorted.
Comparing By Attributes – the concept of comparing is looking for a degree of change. Looking for more or less of a significant attribute.

Ordering By Attributes – the concept or ordering is based on a specific attribute increasing or decreasing. Ordering is a prerequisite for algebra.

Patterning – the core concept of patterning is there are elements repeating.

(Jamieson-Proctor, R. 2016)

Language Model for Pre-Number Understanding:

Language Stage	Materials	Language	Recording
Children’s Language	Lollies, puzzles, card games, toys and counting bears.	‘How can you put these lollies together in threes?’	No symbols, drawing pictures only
Materials language	Lego, blocks and counting bears.	‘How can you put these MAB blocks in groups of four?’	No symbols, drawing pictures only
Maths language	Cubes, MAB blocks and counters.	‘How can you group these twelve objects into groups of four?’ What are the attributes you used in order to sort them?	No symbols.
Symbolic language	No materials and no symbols.	No materials and no symbols.	No materials and no symbols.

Student Misconceptions:

A common misconception that young students have when they are first taught pre-numbers it when subtilizing. The student cannot recognize how many in total are within the group of sorted objects. The student needs to be given ample opportunities to count, make, name and record their collected objects. Through exposure they will being to learn number recognition.

ACARA Links:

Year One

Scootle Resource:

http://www.scootle.edu.au/ec/viewing/R12178/index.html

‘Sorting animals’

This Scootle activity would be best suited for grades one and two. The students would need to use their understanding of attributes to sort the animals into groups and explain their reasoning. This activity would best be suited for a student whom is in the mathematical language stage of the mathematical language model. They would need to know how to sort attributes and make groups. At this stage they would be beginning to count numbers.

Sourced Resource:

‘Matching Butterfly Card Game’

Matching games: This activity develops the skills of questioning and answering, sorting, defining attributes, matching, concentration and memory. This activity would be a starting point for students to understand how to sort attributes. With this activity, the only caution would be that the children might connect the wrong sides of the butterfly. During this activity the teacher would be supportive and point out the differences in the patterns.

Textbook Reading:

A concept within the textbook for pre-numbers would be classification. This is when a student can are taught how to wort objects. They don’t need to know number symbols when they learn the concept of classification. This is a flexible concept.

Week Seven and Eight Reflections

The Big Idea:

Number and Place Value

The Concept of Place Value

Different Types of Numbers

What Is Dyscalculia?

Cardinal, Ordinal and Nominal Numbers

Zero and Place Value

For students to fully grasp mental computation, they need to have numeracy skills, number sense, number knowledge and useful strategies. Students need to understand the strategy and operation in which they wish to use. When they can demonstrate these things, which is when they have fully grasped mental computation. As well as this, students also need to understand the place value of numbers. Place value is the value of the digit, depending on its place in the number. When the student can fully understand place value, that is when they can understand most mathematical operations and determine the difference between different base systems.

Students need to firstly learn cardinal numbers and then they can learn ordinal numbers. A cardinal number is a number which has a denoting quantity. That is one, two, three, etc. Examples of cardinal numbers is ‘here are four coins’. Whereas, ordinal numbers are first, second and third, etc. Examples of ordinal numbers are ‘She came 2nd in the race’. A nominal number is known as a number which is as a name or to identify something. A nominal number is not an actual number value or position. An example of an ordinal number is the numbers on sporting jerseys, zip codes and model numbers.

What Is Dyscalculia?

This is when someone has severe difficulty in making arithmetical calculations, as a result of brain disorder.

Zero and Place Value

A resource explaining zero and place value.

Personal Reflection:

I had forgotten that learning the value of a numbers place was a thing. As you grow up and learn these nitty gritty concepts get forgotten. As a future teacher, I will ensure that my students fully grasp the concept of place value. This will be done through kinesthetic learning. My future students will have a hands-on approach to understanding this mathematical concept.

The concept of place value:

The concept of place value is the position in which a digit is positioned. It is crucial for a student to understand the importance of place value. This concept helps a student to sort and make sense of various amount of numbers. Place value mats are a useful tool when showing the students, the concept of place value. The students are able to move the cubes to change the place value of the number.

The concepts of:

Cardinal numbers: Are known as counting numbers. They show quantity. ‘8 rabbits’ or ’15 dogs’

Ordinal numbers: Tell the order of things in a set. ‘First, second, third’. Ordinal numbers do not show quantity, they only show the numbers rank and position.

Nominal numbers: Are names of something, they identify certain things. They do not show quantity or ranking.

Language Model for Place Value:

Language Stage	Materials	Language	Recording
Children’s Language	Lego, jelly beans, blocks.	‘If I have seven pineapples, how many can I fit in the ones house?’	No symbols, drawing pictures only
Materials language	Magnets, counter bears, blocks and Duplo.	‘If I have 20 pineapples, how many can I fit in the tens house?’	No symbols, drawing pictures only
Maths language	Cubes, MAB blocks and counters.	‘I have 25 pineapples, on the place value mat, we need to move the 20 into the tens house and the five into the ones house’	No symbols.
Symbolic language	No materials and no symbols.	Number place value is shown.	Number place value is used.

Student Misconceptions:

A common misconception which occurs is that students are counting orally and are thinking that big numbers like 468 are: 400 ones, 60 ones and 8 ones. Whereas, the student should be saying: 400 hundred, 60 tens and 8 ones. If the student isn’t able to sort them into the correct place value, they might not fully understand the concept. That is why place value mats are crucial when explaining the concept of place value.

ACARA Links:

Number and algebra. Grade one.

Scootle resource:

https://content.echalk.co.uk/esa/Maths/units/units.html

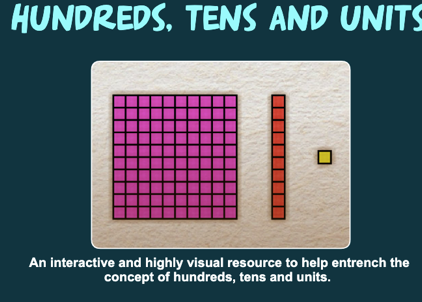
This Scootle resource enables the student to count by partitioning numbers, as well as representing numbers visually by using grids of tens, hundreds and units. This activity would be best suited for grades one and two. This would be best for students whom are in the symbolic language stage of the mathematical language model.

Sourced resource:

This activity would involve the students being given MAB cubes of tens, hundreds and ones. The students would then be asked to sort the blocks into their place value. The only caution to this activity would be if the student got confused with 10 one’s blocks. They would have to be reminded that one’s there are ten ones, they can then be moved into the tens column.

Textbook Reading:

Within the textbook (Reys et al., Chap 8), the students learn about Mrs. Tens and Mrs. Ones role play. This would be a helpful way to incorporate the concept of place value into a physical activity. Through this type of activity, the students would have a visual representation of how number and place value works.

ACARA Links for Foundation Years:

Cardinal, Ordinal and Numerical Numbers

Establish understanding of the language and processes of counting by naming numbers in sequences, initially to and from 20, moving from any starting point (ACMNA001)

Connect number names, numerals and quantities, including zero, initially up to 10 and then beyond (ACMNA002)

Subitise small collections of objects (ACMNA003)

Compare, order and make correspondences between collections, initially to 20, and explain reasoning (ACMNA289)

Foundations Year: Number and Place Value:

Scootle Resource:

http://education.abc.net.au/home#!/media/1150449/counting-and-representing-numbers-1%E2%80%9320

This resource would be best suited to the primary years. This activity uses familiar objects that name, match, compare and order numbers to 20. It also uses addition and subtraction. As well as relating number sentences to the operations. This would be ideal for foundation students whom are at the symbolic stage. They would need to understand numbers and how to read them. This Scootle resource covers sequences (number patterns), positive integers, zero, subtilizing, numerical order, addition and subtraction.

Sourced Resource:

This resource would be best suited for student within lower primary. This activity would help them to understand ordinal numbers. This activity would show a visual representation of numbers 1-10.

ACARA Codes ACMNA027

https://www.teachthis.com.au/products/ordinal-numbers-cards

Textbook Reading:

Chap. 8 (page 216) this chapter compares and contrasts how place values concepts and skills align into the language model of Mathematical development. This was an insightful chapter that gave a range of knowledge on place value.

Week Nine and Ten Reflections

The Big Idea:

Pre-Algebra and Early-Algebra/ Algebra

Determining Relationships within a Pattern

A Definition of Algebra

Solving Simple Algebraic Equations

The difference between algebra and pre-algebra is that pre-algebra takes introduces concepts slower and does not cover as much material as standard algebra. This week’s focus is pre numbers, five counting principles and understanding patterns. For a student to understand algebra, they firstly need to understand relationships and patterns.

Personal Reflection:

I had never considered to reflect upon knowledge of pre-numbers when making meaning of early algebra. I had also never really considered that there was an early algebra. I feel that through learning about pre-algebra, I would be able to confidently teach my future students.

Pre-Algebra Concept:

Pre-algebra as a concept is the ability to understand relationships and patterns. Students must also build an ability to understand how to build a number. Students are firstly introduced by classroom discussion of the relationships; they then would be introduced to symbols to explain the relationships.

Mathematical Language Model for Algebra:

Language Stage	Materials	Language	Recording
Children’s Language	Scales, weight would be used by objects the students are familiar with. This would be in the form of counting bears, magnets and lollies.	‘Patterns’, ‘repeat’, ‘missing’, ‘replace’	No symbols, drawing pictures only
Materials Language	Scales, blocks and shapes.	‘Patterns’, ‘repeat’, ‘missing’, ‘replace’, ‘changing’	No symbols, drawing pictures only
Maths Language	Unifix blocks and MAB blocks	Patterns, relationships, equations,	No symbols, drawing pictures only.
Symbolic Language	Equations and symbols	5+ Z= 20 8 x A= 30	5+ Z= 20 8 x A= 30

Student Misconceptions:

A common misconception that students have about algebra is that it makes maths ‘harder’. Many students see that the equation has a letter in it, and they jump to the conclusion that it must mean that it’s hard. However, algebra uses patterns and inverse operations to find the unknown value. For a student to not think algebra is hard, they need to be shown from the beginning that they can use previously learnt concepts in order to understand algebra.

ACARA Links:

Year One:

Scootle Resource:

This Scootle activity is for students in their foundation years and grade one. Within the activity the students create a sound pattern that is equivalent to a given visual pattern. The concepts within this Scootle activity are pattern perception, comparative language and equivalence. This activity would be best suited for children within the mathematical stage of the language model.

http://www.scootle.edu.au/ec/viewing/L1056/index.html

Sourced Resource:

Algebra Activity

This activity would require the students to know the symbolic language within the language model. They would have to be able to work out the algebra equations in order to balance the scale. This would be a useful tool for the students to visually see how an algebraic equation needs to equal on both sides.

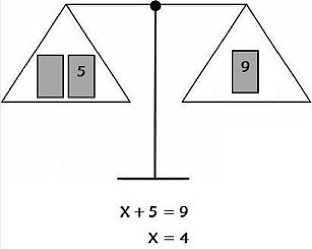
https://www.learn-with-math-games.com/algebra-activities.html

Pre-Algebra Activity:

During this activity the student would be shown the patterns. They would then be asked a series of questions such as ‘what is missing in my pattern?’ and ‘what would be the next step in my pattern’. This activity is suited best for students learning early/ pre-algebra. For this activity they would be using language from the mathematical language stage of the model. A caution that might arise within this activity is that the student might need prompting in what they think will go next. The teacher might have to point out what’s common within the pattern.

Textbook Reading:

Within the textbook it refers to algebra as implementing crucial parts of the curriculum. This is done in the form or patters and problems. This page talks about how to bring in the concept of algebraic thinking for the student. Page 359 (Reys at el., 2012) This is an extremely important knowledge about teaching the concepts of algebra.

Week Eleven Reflections

The Big Idea:

Measurement and the Four Important Teaching Sequences for Measurement

Measurement is best described by measuring something by its size, length or its amount (Siemon, D., Beswick, K., Brady, K., Clark, J., Faragher, R., & Warren, E., 2015). For a student to fully understand measurement, they need to be able to count. As well as the concept of counting, students need to be able to understand the term place value. That is why it is crucial for the students to understand these concepts fully before they are introduced to the concept of measurement.

Four Teaching Sequences for Measurement:

1. Identifying The Attribute
2. Choosing The Appropriate Unit Of Measurement
3. Measuring The Object With The Chosen Unit
4. Reporting The Number Of Units

Personal Reflection:

I was not aware at first that in order for a child to be able to understand measurement, they would need to understand many other concepts. As a future teacher, I’m required to know that students need to be able to comprehend various principles, in order to understand the concept of measurement.

The Concept of Measurement:

The concept of measurement is for the student to be able to count units. This concept would be taught to the students using the four teaching sequences for measurement. The teacher would decide at what point in time they would teach these steps to the students. When introducing the unit of measurement to students, the language model would be used. This would help the teacher to determine where the student’s level of knowledge is at.

Language Model for Measurement:

Language Stage	Materials	Language	Recording
Children’s Language	Toys, Lego, chocolates, lollies and small cars.	‘Longer’, ‘thicker’, ‘thinner’, ‘shorter’, ‘skinnier’, ‘wider’	No symbols, drawing pictures only.
materials language	Counters, MAB blocks, cubes, buttons, marbles, paper clips and unfix cubes	‘Longer’, ‘thicker’, ‘thinner’, ‘shorter’, ‘skinnier’, ‘wider’	No symbols, drawing pictures only.
maths language	MAB blocks	‘Describe the attributes’, ‘How can you group them’	No symbols, drawing pictures only.
symbolic language	Rulers, tape measures and Google maps.	M, mm, cm, km	M, mm, cm, km

Student Misconceptions:

A common misconception which occurs for students when studying measurement, is that they don’t line their ruler or measuring tool correctly. The student may start their ruler at one, instead of lining it up with the zero. When the student is within the symbolic stage of learning measurement, this misconception would lead to the student not getting the correct measurements. In order for the students to not gain this misconception, within the early stages of them learning, the teacher should model to the student how to measure. The students should constantly be reminded that they need to start at zero when measuring. They could have weekly assessments for the teacher to check their understanding of this.

ACARA Links:

Grade One:

Scootle Resource:

https://www.pbslearningmedia.org/resource/619d53ff-1c4b-46bf-9082-0fa97a397576/treasure-map-peg-cat/

This Scootle resource would be aimed at children within years one and two. The students would need to be in the symbolic stage of the mathematical language model. They would need to be able to measure within their resource and understand measurement symbols.

Sourced Resource:

This resource would be aimed at year one students. They would need to be in the symbolic stage of the mathematical language model. For this activity they would be required to measure with a ruler the length of the objects on the page.

https://www.teacherspayteachers.com/Product/FREE-Measurement-Game-1799577

Textbook Reading:

The textbook refers to measurement being found in our everyday lives. There are various ways measurement is used within a student’s everyday lives. On page 406 of the textbook (Reys at el., 2012) it describes the teaching strategies needed for the concept of comparing length and physical objects. It demonstrated how a teacher would ask their students to compare lengths by asking certain questions.

Week twelve reflection

The Big Idea:

Geometry: Three Dimensional Shapes, Two Dimensional Shapes, How Children Learn Geometry and Geometry Skills

Geometry involves the properties and relations of lines, points, surfaces and dimensional analogues. Geometry is better known as the study of shapes, measurement and space. (Roth, W., 2011). It teaches students how to create 2D, 3D and 1D shapes. When teaching the unit geometry to students, the teacher needs to be aware that they use the right language for the language level the students are firstly in.

Personal Reflection:

When I learnt geometry, I found it hard to remember all the terms and the names of all the shapes. As a future teacher, I do not want my students to feel the way that I did when I was in schooling. That is why I believe that the student would best learn geometry through kinaesthetic learning. They need to be hands on with all tasks. This enables the students to fully understand the concept of geometry. In order for students to thrive within this unit, they need to be provided with many various resources. I would first introduce let them touch and look at all 1D, 2D and 3D shapes. They would see what they look like and be able to touch them. From there I would build their knowledge of geometry through teaching them through activities such as ‘building a paper town’.

Concepts of Geometry:

In order for students to understand the concept of geometry and its shapes, they need to begin through playing and making meaning. When teaching students geometry, the mathematical language model needs to be used. The concept of geometry is an organised, logical and coherent system for the study of shapes, space and measurement (Jamison-Proctor)

Mathematical Language Model for Geometry:

Language Stages	Materials	Language	Recording
Student’s Language	paper, cardboard, playdough	‘Edges’, ‘angle’, ‘outside’, ‘inside’	No symbols, children drawing pictures only.
Materials Language	Pipe cleaners, pen and paper	‘Edges’, ‘angle’, ‘outside’, ‘inside’, ‘beside’, ‘between’	No symbols, children drawing pictures only.
Maths Language	Nets or templates of the shapes.	‘faces’, ‘perimeter’, ‘circumference’, ‘capacity’, ‘length’, ‘width’, ‘height’	No symbols, children drawing pictures only.
Symbolic Language	Formulas	‘capacity’, ‘faces’, formulas, ‘perimeter’, ‘volume’	Formulas

Student Misconceptions:

Within geometry common misconceptions can be avoided. This would be done by the teacher planning carefully how they would present the information to the students. Students form misconceptions in geometry when they are shown shapes always in one certain position. When presented with a shape which is deemed ‘upside down’ to the student, they may get confused. That is why to abolish this confusion, the teacher needs to present shapes in a range of different orientations. (Claire Mooney, 2018)

Acara Links:

For Grade One:

Scootle Resource:

This Scootle resource would best be suited for students within prep and grades one-two. This recourse enables the students to manipulate shapes through sliding and overlapping in order to create shapes. It assesses the student’s concepts in pattern perception, geometry properties, shape perception and simple shapes. For this activity, a student within the mathematical leaning stage of the language model would be able to complete this. (Scootle, 2019)

http://www.scootle.edu.au/ec/viewing/L752/index.html

Sourced Resource:

‘Shape crossword’ is an activity that enables the students to test their knowledge of the two dimensional and three-dimensional shapes. They need to fill in the black squares with the names of all the shapes. This activity would best be suited for a student that was in the mathematical language stage of the mathematical language model. In order for them to know the shape, they would need to be able to figure out how many sides it had.

http://www.mathblaster.com/teachers/math-practice/math-lesson-plans/shapeword-crossword-view

Textbook Reading:

The textbook refers to the building the students learning through physically building 2D and 3D shapes. This is known as ‘edge models’. This would be best suited to upper primary students. Students would learn this when they had acquired knowledge on how they will build these types of shapes. (Reys at el., 2012, p.380)

Reference list:

ACARA. (2019). Retrieved from https://www.australiancurriculum.edu.au/f-10-

curriculum/Mathematics/

APASS education. (2019). 4 Common Misconceptions Students Have About Subtraction. Retrieved from APASS education: https://apasseducation.com/4-misconceptions-students-about-subtraction/

Burnett, J., Irons, C., & Turton, A. (2015). Subtraction: A comprehensive guide for teaching

subtraction facts (Book of facts).

Claire Mooney, M. B. (2018). Primary mathematics 8th edition Teaching theory and Practice . London: SAGE. Retrieved from https://uk.sagepub.com/sites/default/files/upm-binaries/90770_Ch6_children%27s_common_mathematical_misconceptions.pdf

Cockburn, A. D. (2007). Understanding subtraction through enhanced

communication. Mathematical Understanding 5-11: A Practical Guide to Creative Communication in Maths, 9.

Division (In Mathematics). (2001). Dictionary of Engineering Terms, Butterworth-

Heinemann.

Place Value. (2012). Two Sisters Teach. Retrieved from

http://twosistersteach.blogspot.com/2012/09/place-value.html

Reys, R., Lindquist, M., Lambdin, D., Smith, N., Rogers, A., Falle, J., Frid, S., & Bennett, S.

(2012). Helping children learn Mathematics (2^nd Australian ed.) Milton: John Wiley & Sons.

Roth, W. (2011). Geometry as objective science in elementary school classrooms

mathematics in the flesh (Routledge international studies in the philosophy of education; 27). New York: Routledge.

Scott, D. (2017). Education Systems and Learners Knowledge and Knowing.

Scootle. (2019). https://www.scootle.edu.au/ec/p/home

Siemon, D., Beswick, K., Brady, K., Clark, J., Faragher, R., & Warren, E. (2015). Teaching

Mathematics: Foundations to middle years (Second ed.).

Wells, D. (2012). What is Multiplication? Mathematics in School, 41(3), 37-39.